Расчет гипотенузы прямоугольного треугольника в см

Как найти гипотенузу прямоугольного треугольника, если известны его катеты?

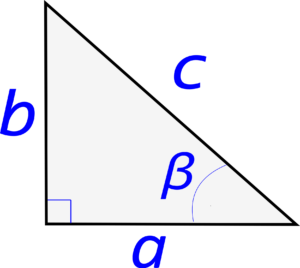
Гипотенуза — это сторона противоположная прямому углу (90 градусов) прямоугольного треугольника, является самой длинной стороной.

Катеты — это стороны прилегающие к прямому углу (90 градусов) прямоугольного треугольника.

Гипотенузу прямоугольного треугольника можно найти по теореме Пифагора: длина гипотенузы в квадрате равна сумме длин катетов в квадрате.

Формула теоремы Пифагора для поиска длины гипотенузы прямоугольного треугольника:

c² = a² + b² ⇒

c = √(a² + b²)

a — известная длина первого катета прямоугольного треугольника в см (сантиметрах);

b — известная длина второго катета прямоугольного треугольника в см (сантиметрах);

c — длина гипотенузы прямоугольного треугольника в см (сантиметрах).

Например:

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 5 см и 12 см.

Краткое решение: c = √(a² + b²) = √(5² + 12²) = 13 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 3 см и 4 см.

Краткое решение: c = √(a² + b²) = √(3² + 4²) = 5 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 6 см и 8 см.

Краткое решение: c = √(a² + b²) = √(6² + 8²) = 10 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 9 см и 12 см.

Краткое решение: c = √(a² + b²) = √(9² + 12²) = 15 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 25 см и 60 см.

Краткое решение: c = √(a² + b²) = √(25² + 60²) = 65 см

Найдите длину гипотенузы прямоугольного треугольника, если его катеты равны 12 см и 16 см.

Краткое решение: c = √(a² + b²) = √(12² + 16²) = 20 см